Menguasai KPK dan FPB: Panduan Lengkap Contoh Soal untuk Kelas 4 SD (Dilengkapi Latihan Praktis Siap Unduh!)
Matematika seringkali dianggap sebagai pelajaran yang menakutkan bagi sebagian siswa. Namun, dengan pendekatan yang tepat dan contoh soal yang relevan, konsep-konsep yang rumit pun bisa menjadi mudah dan menyenangkan. Salah satu materi penting yang diajarkan di kelas 4 Sekolah Dasar adalah Kelipatan Persekutuan Terkecil (KPK) dan Faktor Persekutuan Terbesar (FPB).
Materi ini bukan hanya sekadar angka-angka di buku, tetapi memiliki aplikasi nyata dalam kehidupan sehari-hari, seperti mengatur jadwal, membagi benda secara adil, atau bahkan dalam resep masakan. Artikel ini akan memandu Anda memahami KPK dan FPB dari dasar, dilengkapi dengan berbagai contoh soal, tips belajar, dan latihan praktis yang bisa Anda manfaatkan sebagai bahan ajar.
Pendahuluan: Mengapa KPK dan FPB Penting?
KPK dan FPB adalah fondasi penting dalam pelajaran matematika selanjutnya, terutama saat siswa belajar tentang pecahan, rasio, dan proporsi. Memahami konsep ini sejak dini akan membantu siswa membangun dasar yang kuat untuk materi yang lebih kompleks di jenjang berikutnya. Mari kita selami lebih dalam!
I. Memahami Dasar-Dasar Sebelum Melangkah Jauh
Sebelum kita masuk ke KPK dan FPB, ada beberapa konsep dasar yang harus dikuasai terlebih dahulu oleh siswa kelas 4.
A. Bilangan Prima dan Faktorisasi Prima
- Bilangan Prima: Adalah bilangan asli yang lebih besar dari 1 dan hanya memiliki dua faktor, yaitu 1 dan bilangan itu sendiri.
- Contoh: 2, 3, 5, 7, 11, 13, 17, 19, dst. (Perhatikan, 1 bukan bilangan prima karena hanya memiliki satu faktor).
-
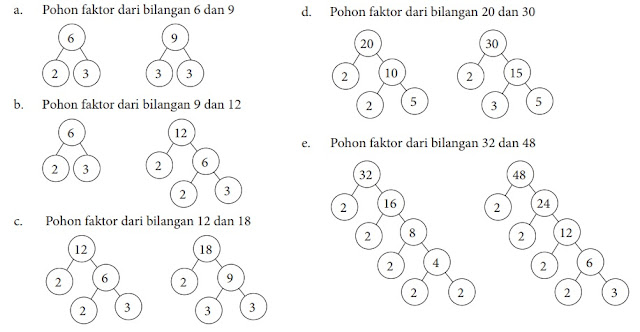
Faktorisasi Prima: Adalah cara menyatakan sebuah bilangan sebagai hasil kali faktor-faktor primanya. Kita bisa menggunakan pohon faktor untuk melakukannya.
-
Contoh Pohon Faktor:
-
Angka 24:
24 / 2 12 / 2 6 / 2 3Jadi, faktorisasi prima dari 24 adalah 2 x 2 x 2 x 3 = 2³ x 3.
-
Angka 36:
36 / 2 18 / 2 9 / 3 3Jadi, faktorisasi prima dari 36 adalah 2 x 2 x 3 x 3 = 2² x 3².
-
-
B. Faktor dan Kelipatan
- Faktor Suatu Bilangan: Adalah bilangan-bilangan yang dapat membagi habis bilangan tersebut tanpa sisa.
- Contoh:
- Faktor dari 12: 1, 2, 3, 4, 6, 12 (karena 12:1=12, 12:2=6, dst.)
- Faktor dari 18: 1, 2, 3, 6, 9, 18
- Contoh:
- Kelipatan Suatu Bilangan: Adalah hasil perkalian bilangan tersebut dengan bilangan asli (1, 2, 3, dst.).
- Contoh:
- Kelipatan dari 4: 4, 8, 12, 16, 20, 24, 28, 32, 36, dst. (4×1, 4×2, 4×3, dst.)
- Kelipatan dari 6: 6, 12, 18, 24, 30, 36, dst.
- Contoh:
II. Kelipatan Persekutuan Terkecil (KPK)
A. Apa itu KPK?
KPK adalah Kelipatan Persekutuan Terkecil. Ini berarti kita mencari kelipatan yang sama (persekutuan) dari dua atau lebih bilangan, lalu memilih yang nilainya paling kecil.
B. Metode Menentukan KPK
Ada beberapa metode yang bisa digunakan untuk menentukan KPK. Untuk kelas 4, metode daftar kelipatan dan faktorisasi prima adalah yang paling umum.
1. Metode Daftar Kelipatan (untuk bilangan kecil):
- Tuliskan kelipatan dari masing-masing bilangan.
- Cari kelipatan yang sama (persekutuan).
-
Pilih kelipatan persekutuan yang paling kecil.
Contoh Soal 1: Tentukan KPK dari 4 dan 6.
- Kelipatan 4: 4, 8, 12, 16, 20, 24, 28, …
- Kelipatan 6: 6, 12, 18, 24, 30, …
- Kelipatan persekutuan 4 dan 6 adalah 12, 24, …
- KPK dari 4 dan 6 adalah 12.
2. Metode Faktorisasi Prima (lebih efektif untuk bilangan besar):
- Lakukan faktorisasi prima untuk setiap bilangan menggunakan pohon faktor.
- Tuliskan hasil faktorisasi prima dalam bentuk perkalian faktor-faktor primanya.
-
Untuk mencari KPK, kalikan semua faktor prima yang ada (baik yang sama maupun yang tidak sama). Jika ada faktor prima yang sama, ambil pangkat yang terbesar.
Contoh Soal 2: Tentukan KPK dari 12 dan 18.
- Faktorisasi prima 12: 2² x 3
- Faktorisasi prima 18: 2 x 3²
- Faktor prima yang ada: 2 dan 3.
- Ambil pangkat terbesar untuk 2: 2²
- Ambil pangkat terbesar untuk 3: 3²
- KPK = 2² x 3² = 4 x 9 = 36.
3. Metode Tabel / Sengkedan (alternatif lain):
- Tuliskan bilangan-bilangan dalam sebuah tabel.
- Bagi bilangan-bilangan tersebut dengan bilangan prima terkecil yang bisa membagi salah satunya (atau keduanya).
- Lingkari pembagi jika bisa membagi semua bilangan.
- Terus bagi hingga semua bilangan menjadi 1.
-
KPK adalah hasil kali semua pembagi.
Contoh Soal 3: Tentukan KPK dari 12 dan 18.
Pembagi | 12 | 18 --------|----|---- 2 | 6 | 9 (Lingkari 2 karena membagi keduanya) 2 | 3 | 9 3 | 1 | 3 (Lingkari 3 karena membagi keduanya) 3 | 1 | 1KPK = 2 x 2 x 3 x 3 = 2² x 3² = 4 x 9 = 36.
III. Faktor Persekutuan Terbesar (FPB)
A. Apa itu FPB?
FPB adalah Faktor Persekutuan Terbesar. Ini berarti kita mencari faktor yang sama (persekutuan) dari dua atau lebih bilangan, lalu memilih yang nilainya paling besar.
B. Metode Menentukan FPB
Mirip dengan KPK, ada beberapa metode untuk FPB.
1. Metode Daftar Faktor (untuk bilangan kecil):
- Tuliskan semua faktor dari masing-masing bilangan.
- Cari faktor yang sama (persekutuan).
-
Pilih faktor persekutuan yang paling besar.
Contoh Soal 4: Tentukan FPB dari 12 dan 18.
- Faktor dari 12: 1, 2, 3, 4, 6, 12
- Faktor dari 18: 1, 2, 3, 6, 9, 18
- Faktor persekutuan 12 dan 18 adalah 1, 2, 3, 6.
- FPB dari 12 dan 18 adalah 6.
2. Metode Faktorisasi Prima (lebih efektif untuk bilangan besar):
- Lakukan faktorisasi prima untuk setiap bilangan.
- Tuliskan hasil faktorisasi prima.
-
Untuk mencari FPB, kalikan faktor prima yang sama saja. Jika ada faktor prima yang sama, ambil pangkat yang terkecil.
Contoh Soal 5: Tentukan FPB dari 24 dan 36.
- Faktorisasi prima 24: 2³ x 3
- Faktorisasi prima 36: 2² x 3²
- Faktor prima yang sama: 2 dan 3.
- Ambil pangkat terkecil untuk 2: 2²
- Ambil pangkat terkecil untuk 3: 3¹
- FPB = 2² x 3 = 4 x 3 = 12.
3. Metode Tabel / Sengkedan (alternatif lain):
-
Sama seperti KPK, tetapi untuk FPB, kalikan hanya pembagi yang bisa membagi semua bilangan pada baris tersebut (yang dilingkari jika Anda menggunakan metode melingkari).
Contoh Soal 6: Tentukan FPB dari 24 dan 36.
Pembagi | 24 | 36 --------|----|---- 2 | 12 | 18 (Lingkari 2 karena membagi keduanya) 2 | 6 | 9 (Lingkari 2 karena membagi keduanya) 3 | 2 | 3 (Lingkari 3 karena membagi keduanya)FPB = 2 x 2 x 3 = 4 x 3 = 12.
IV. Mengaplikasikan KPK dan FPB dalam Soal Cerita
Soal cerita adalah bagian terpenting karena menguji pemahaman siswa tentang kapan harus menggunakan KPK dan kapan harus menggunakan FPB dalam konteks kehidupan nyata.
A. Ciri-ciri Soal Cerita KPK:
- Biasanya menanyakan waktu atau jumlah minimal suatu kejadian yang akan terjadi bersama-sama lagi.
-
Kata kunci: "setiap … sekali", "bersama-sama lagi", "kapan akan bertemu lagi", "paling sedikit".
Contoh Soal Cerita KPK 1:
Lampu A menyala setiap 6 detik sekali, dan lampu B menyala setiap 8 detik sekali. Jika kedua lampu menyala bersamaan pada pukul 08.00, pada detik ke berapa lagi kedua lampu akan menyala bersamaan?- Identifikasi: Kata kunci "bersama-sama lagi" menunjukkan ini adalah soal KPK.
- Penyelesaian: Cari KPK dari 6 dan 8.
- Faktorisasi prima 6 = 2 x 3
- Faktorisasi prima 8 = 2³
- KPK = 2³ x 3 = 8 x 3 = 24.
- Jadi: Kedua lampu akan menyala bersamaan lagi pada detik ke-24.
Contoh Soal Cerita KPK 2:
Ani berenang setiap 4 hari sekali, sedangkan Budi berenang setiap 6 hari sekali. Jika pada tanggal 1 Mei mereka berenang bersama-sama, pada tanggal berapa mereka akan berenang bersama-sama lagi?- Identifikasi: Kata kunci "bersama-sama lagi" menunjukkan ini adalah soal KPK.
- Penyelesaian: Cari KPK dari 4 dan 6.
- Faktorisasi prima 4 = 2²
- Faktorisasi prima 6 = 2 x 3
- KPK = 2² x 3 = 4 x 3 = 12.
- Mereka akan berenang bersama-sama lagi 12 hari setelah 1 Mei.
- 1 Mei + 12 hari = 13 Mei.
- Jadi: Ani dan Budi akan berenang bersama-sama lagi pada tanggal 13 Mei.
B. Ciri-ciri Soal Cerita FPB:
- Biasanya menanyakan jumlah kelompok terbanyak, ukuran terbesar, atau berapa banyak yang bisa dibagi rata ke setiap orang/kelompok.
-
Kata kunci: "paling banyak", "terbanyak", "ukuran terbesar", "jumlah yang sama", "dibagi rata", "masing-masing mendapatkan".
Contoh Soal Cerita FPB 1:
Ibu memiliki 20 kue bolu dan 30 kue lapis. Kue-kue tersebut akan dimasukkan ke dalam kotak dengan jumlah masing-masing jenis kue sama banyak di setiap kotak. Berapa kotak terbanyak yang dapat dibuat Ibu?- Identifikasi: Kata kunci "jumlah masing-masing jenis kue sama banyak" dan "berapa kotak terbanyak" menunjukkan ini adalah soal FPB.
- Penyelesaian: Cari FPB dari 20 dan 30.
- Faktorisasi prima 20 = 2² x 5
- Faktorisasi prima 30 = 2 x 3 x 5
- FPB = 2 x 5 = 10.
- Jadi: Ibu dapat membuat 10 kotak terbanyak. (Setiap kotak berisi 20:10=2 kue bolu dan 30:10=3 kue lapis).
Contoh Soal Cerita FPB 2:
Pak Budi memiliki 45 pensil dan 60 buku. Beliau ingin membagikan pensil dan buku tersebut kepada anak-anak panti asuhan sehingga setiap anak mendapatkan jumlah pensil dan buku yang sama banyak. Berapa anak terbanyak yang dapat menerima pensil dan buku dari Pak Budi?- Identifikasi: Kata kunci "setiap anak mendapatkan jumlah … yang sama banyak" dan "berapa anak terbanyak" menunjukkan ini adalah soal FPB.
- Penyelesaian: Cari FPB dari 45 dan 60.
- Faktorisasi prima 45 = 3² x 5
- Faktorisasi prima 60 = 2² x 3 x 5
- FPB = 3 x 5 = 15.
- Jadi: Pak Budi dapat membagikan pensil dan buku kepada 15 anak terbanyak. (Setiap anak akan mendapatkan 45:15=3 pensil dan 60:15=4 buku).
V. Kumpulan Soal Latihan (Siap untuk Dijadikan PDF!)
Berikut adalah beberapa soal latihan yang bisa Anda gunakan untuk melatih pemahaman siswa. Anda bisa menyalinnya dan membuat lembar kerja PDF untuk dicetak.
A. Soal KPK:
- Tentukan KPK dari 9 dan 12.
- Tentukan KPK dari 15 dan 25.
- Tentukan KPK dari 8, 12, dan 16.
- Bus A berangkat dari terminal setiap 15 menit, dan Bus B berangkat setiap 20 menit. Jika kedua bus berangkat bersama pada pukul 07.00, pada pukul berapa lagi kedua bus akan berangkat bersama?
- Dita les matematika setiap 3 hari sekali dan les piano setiap 5 hari sekali. Jika pada tanggal 10 April Dita les keduanya, pada tanggal berapa lagi Dita akan les matematika dan piano bersamaan?
B. Soal FPB:
- Tentukan FPB dari 28 dan 42.
- Tentukan FPB dari 50 dan 75.
- Tentukan FPB dari 36, 48, dan 60.
- Pak Arman memiliki 24 buah jeruk dan 32 buah apel. Buah-buahan tersebut akan dimasukkan ke dalam keranjang dengan jumlah yang sama banyak untuk setiap jenis. Berapa keranjang terbanyak yang bisa dibuat Pak Arman?
- Di sebuah perpustakaan, terdapat 72 buku cerita dan 96 buku pelajaran. Buku-buku tersebut akan disusun di rak-rak sehingga setiap rak memiliki jumlah buku cerita dan buku pelajaran yang sama banyak. Berapa rak terbanyak yang dibutuhkan?
VI. Tips Tambahan untuk Orang Tua dan Guru:
- Mulai dari Dasar: Pastikan siswa benar-benar memahami konsep bilangan prima, faktor, dan kelipatan sebelum melangkah ke KPK dan FPB.
- Visualisasi: Gunakan alat bantu visual seperti blok bangunan, kelereng, atau gambar untuk membantu siswa memvisualisasikan konsep faktor dan kelipatan.
- Real-World Connection: Berikan contoh-contoh soal cerita yang relevan dengan kehidupan sehari-hari siswa agar mereka merasa bahwa matematika itu berguna.
- Latihan Konsisten: Latihan secara teratur adalah kunci. Mulai dari soal mudah, lalu bertahap ke soal yang lebih menantang.
- Pohon Faktor itu Penting: Tekankan penggunaan pohon faktor karena ini adalah metode paling sistematis untuk menemukan faktorisasi prima, yang sangat membantu dalam menentukan KPK dan FPB untuk bilangan yang lebih besar.
- Jangan Terburu-buru: Biarkan siswa memahami satu konsep sepenuhnya sebelum beralih ke konsep berikutnya. Kesabaran adalah kunci.
Penutup
Menguasai KPK dan FPB di kelas 4 SD adalah langkah awal yang sangat baik dalam perjalanan belajar matematika siswa. Dengan penjelasan yang jelas, contoh-contoh yang bervariasi, dan latihan yang konsisten, siswa akan mampu memahami dan mengaplikasikan konsep ini dengan percaya diri. Semoga artikel ini bermanfaat sebagai panduan lengkap bagi siswa, orang tua, dan guru dalam mempelajari KPK dan FPB. Selamat belajar!
