Menguak Rahasia KPK dan FPB: Belajar Asyik Matematika untuk Kelas 4 SD!

Halo, Adik-adik hebat calon matematikawan! Apa kabar? Semoga selalu semangat belajar, ya! Hari ini, kita akan memulai petualangan seru di dunia matematika, khususnya tentang dua sahabat karib yang sering muncul bersama: KPK (Kelipatan Persekutuan Terkecil) dan FPB (Faktor Persekutuan Terbesar).

Mungkin sebagian dari kalian pernah mendengar atau bahkan sedikit bingung dengan kedua istilah ini. Tenang saja! Di artikel ini, kita akan belajar bersama dengan cara yang paling asyik, lengkap dengan contoh-contoh soal yang mudah dipahami. Siap? Yuk, kita mulai!

Kenapa Sih Kita Perlu Belajar KPK dan FPB?

KPK dan FPB ini bukan cuma angka-angka di buku pelajaran, lho! Mereka punya banyak kegunaan dalam kehidupan kita sehari-hari. Misalnya, saat kita ingin mengatur jadwal bus yang berangkat bersamaan, atau membagi permen dan cokelat secara adil kepada teman-teman. Seru, kan?

Sebelum kita masuk ke KPK dan FPB, ada beberapa konsep dasar yang harus kita pahami dulu. Ini seperti fondasi rumah, harus kuat agar bangunannya kokoh.

Fondasi Penting: Memahami Konsep Dasar

1. Bilangan Prima

Pernah dengar kata "prima"? Bukan nama orang, ya! Dalam matematika, bilangan prima adalah bilangan asli yang lebih besar dari 1 dan hanya bisa dibagi oleh 1 dan dirinya sendiri.

Contoh bilangan prima:

• 2: Hanya bisa dibagi 1 dan 2. (Ini satu-satunya bilangan prima genap, lho!)
• 3: Hanya bisa dibagi 1 dan 3.
• 5: Hanya bisa dibagi 1 dan 5.
• 7: Hanya bisa dibagi 1 dan 7.
• 11: Hanya bisa dibagi 1 dan 11.
• …dan seterusnya.

Bukan bilangan prima contohnya:

• 4: Bisa dibagi 1, 2, dan 4. (Ada angka 2 selain 1 dan 4).
• 6: Bisa dibagi 1, 2, 3, dan 6.
• 9: Bisa dibagi 1, 3, dan 9.

2. Faktorisasi Prima

Setelah tahu apa itu bilangan prima, sekarang kita belajar faktorisasi prima. Ini adalah cara mengubah sebuah bilangan menjadi perkalian dari bilangan-bilangan primanya. Alat bantunya yang paling terkenal adalah pohon faktor.

Contoh 1: Faktorisasi Prima dari 12

    12
   /  
  2    6
       / 
      2   3

• Kita mulai dari 12. Cari bilangan prima terkecil yang bisa membagi 12, yaitu 2.
• 12 dibagi 2 hasilnya 6.
• Sekarang, kita fokus ke 6. Cari bilangan prima terkecil yang bisa membagi 6, yaitu 2.
• 6 dibagi 2 hasilnya 3.
• Angka 3 adalah bilangan prima, jadi kita berhenti.
• Jadi, faktorisasi prima dari 12 adalah 2 x 2 x 3 atau bisa ditulis 2² x 3.

Contoh 2: Faktorisasi Prima dari 30

    30
   /  
  2    15
       /  
      3    5

• 30 dibagi 2 hasilnya 15.
• 15 tidak bisa dibagi 2. Coba bilangan prima selanjutnya, yaitu 3.
• 15 dibagi 3 hasilnya 5.
• Angka 5 adalah bilangan prima, jadi kita berhenti.
• Jadi, faktorisasi prima dari 30 adalah 2 x 3 x 5.

3. Kelipatan Bilangan

Kelipatan suatu bilangan adalah hasil perkalian bilangan tersebut dengan bilangan asli (1, 2, 3, 4, dst). Gampangannya, seperti kita menghitung loncat.

Contoh 1: Kelipatan dari 4

• 4 x 1 = 4
• 4 x 2 = 8
• 4 x 3 = 12
• 4 x 4 = 16
• …dan seterusnya.
  Jadi, kelipatan 4 adalah: 4, 8, 12, 16, 20, 24, 28, 32, …

Contoh 2: Kelipatan dari 5

• 5 x 1 = 5
• 5 x 2 = 10
• 5 x 3 = 15
• 5 x 4 = 20
• …dan seterusnya.
  Jadi, kelipatan 5 adalah: 5, 10, 15, 20, 25, 30, …

4. Faktor Bilangan

Faktor suatu bilangan adalah semua bilangan yang bisa membagi habis bilangan tersebut.

Contoh 1: Faktor dari 12
Kita cari angka berapa saja yang bisa membagi 12 tanpa sisa.

• 12 : 1 = 12
• 12 : 2 = 6
• 12 : 3 = 4
• 12 : 4 = 3
• 12 : 6 = 2
• 12 : 12 = 1
  Jadi, faktor dari 12 adalah: 1, 2, 3, 4, 6, dan 12.

Contoh 2: Faktor dari 18

• 18 : 1 = 18
• 18 : 2 = 9
• 18 : 3 = 6
• 18 : 6 = 3
• 18 : 9 = 2
• 18 : 18 = 1
  Jadi, faktor dari 18 adalah: 1, 2, 3, 6, 9, dan 18.

Mengenal KPK (Kelipatan Persekutuan Terkecil)

KPK adalah kelipatan yang sama dari dua bilangan atau lebih, dan nilainya paling kecil (selain nol).

Ada dua cara untuk mencari KPK:

Cara 1: Mendaftar Kelipatan (Cocok untuk angka kecil)

Contoh Soal 1: Berapakah KPK dari 4 dan 6?

1. Daftar kelipatan 4: 4, 8, 12, 16, 20, 24, …
2. Daftar kelipatan 6: 6, 12, 18, 24, 30, …

• Kelipatan yang sama (persekutuan) dari 4 dan 6 adalah 12, 24, …
• Kelipatan persekutuan yang paling kecil (terkecil) adalah 12.
• Jadi, KPK dari 4 dan 6 adalah 12.

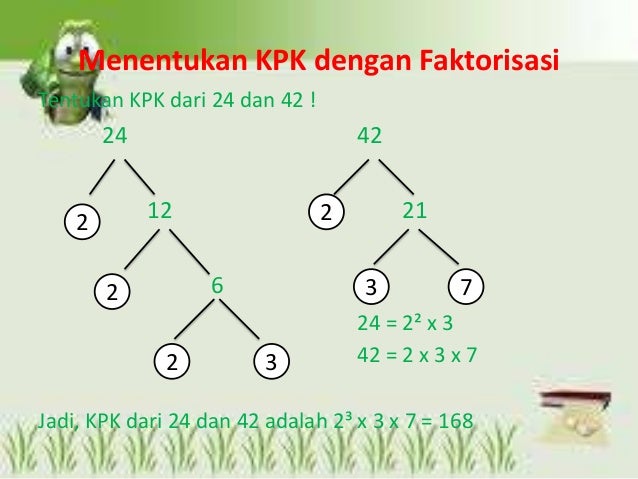
Cara 2: Menggunakan Faktorisasi Prima (Cara paling efektif)

Langkah-langkah mencari KPK dengan faktorisasi prima:

1. Buat faktorisasi prima untuk setiap bilangan menggunakan pohon faktor.
2. Kalikan semua faktor prima yang ada.
3. Jika ada faktor prima yang sama, ambil yang pangkatnya paling besar.

Contoh Soal 2: Berapakah KPK dari 8 dan 12?

1. Faktorisasi Prima:

   • 8 = 2 x 2 x 2 = 2³
   • 12 = 2 x 2 x 3 = 2² x 3

2. Pilih faktor prima:

   • Ada faktor 2 dan 3.
   • Untuk faktor 2, ada 2³ dan 2². Kita pilih yang pangkatnya paling besar, yaitu 2³.
   • Untuk faktor 3, hanya ada 3.

3. Hitung KPK:

   • KPK = 2³ x 3
   • KPK = (2 x 2 x 2) x 3
   • KPK = 8 x 3 = 24

Contoh Soal 3: Berapakah KPK dari 15 dan 20?

1. Faktorisasi Prima:

   • 15 = 3 x 5
   • 20 = 2 x 2 x 5 = 2² x 5

2. Pilih faktor prima:

   • Ada faktor 2, 3, dan 5.
   • Untuk faktor 2, hanya ada 2².
   • Untuk faktor 3, hanya ada 3.
   • Untuk faktor 5, ada 5 (dari 15) dan 5 (dari 20). Keduanya pangkat 1, jadi kita ambil 5.

3. Hitung KPK:

   • KPK = 2² x 3 x 5
   • KPK = (2 x 2) x 3 x 5
   • KPK = 4 x 3 x 5
   • KPK = 12 x 5 = 60

Contoh Soal 4: Berapakah KPK dari 6, 9, dan 12?

1. Faktorisasi Prima:

   • 6 = 2 x 3
   • 9 = 3 x 3 = 3²
   • 12 = 2 x 2 x 3 = 2² x 3

2. Pilih faktor prima:

   • Ada faktor 2 dan 3.
   • Untuk faktor 2, ada 2 (dari 6) dan 2² (dari 12). Kita pilih yang pangkatnya paling besar, yaitu 2².
   • Untuk faktor 3, ada 3 (dari 6 dan 12) dan 3² (dari 9). Kita pilih yang pangkatnya paling besar, yaitu 3².

3. Hitung KPK:

   • KPK = 2² x 3²
   • KPK = (2 x 2) x (3 x 3)
   • KPK = 4 x 9 = 36

Mengenal FPB (Faktor Persekutuan Terbesar)

FPB adalah faktor yang sama dari dua bilangan atau lebih, dan nilainya paling besar.

Ada dua cara untuk mencari FPB:

Cara 1: Mendaftar Faktor (Cocok untuk angka kecil)

Contoh Soal 5: Berapakah FPB dari 12 dan 18?

1. Daftar faktor 12: 1, 2, 3, 4, 6, 12
2. Daftar faktor 18: 1, 2, 3, 6, 9, 18

• Faktor yang sama (persekutuan) dari 12 dan 18 adalah 1, 2, 3, 6.
• Faktor persekutuan yang paling besar (terbesar) adalah 6.
• Jadi, FPB dari 12 dan 18 adalah 6.

Cara 2: Menggunakan Faktorisasi Prima (Cara paling efektif)

Langkah-langkah mencari FPB dengan faktorisasi prima:

1. Buat faktorisasi prima untuk setiap bilangan menggunakan pohon faktor.
2. Kalikan faktor prima yang hanya muncul di SEMUA bilangan.
3. Jika ada faktor prima yang sama, ambil yang pangkatnya paling kecil.

Contoh Soal 6: Berapakah FPB dari 24 dan 36?

1. Faktorisasi Prima:

   • 24 = 2 x 2 x 2 x 3 = 2³ x 3
   • 36 = 2 x 2 x 3 x 3 = 2² x 3²

2. Pilih faktor prima:

   • Faktor prima yang muncul di kedua bilangan adalah 2 dan 3.
   • Untuk faktor 2, ada 2³ dan 2². Kita pilih yang pangkatnya paling kecil, yaitu 2².
   • Untuk faktor 3, ada 3 (dari 24) dan 3² (dari 36). Kita pilih yang pangkatnya paling kecil, yaitu 3.

3. Hitung FPB:

   • FPB = 2² x 3
   • FPB = (2 x 2) x 3
   • FPB = 4 x 3 = 12

Contoh Soal 7: Berapakah FPB dari 40 dan 60?

1. Faktorisasi Prima:

   • 40 = 2 x 2 x 2 x 5 = 2³ x 5
   • 60 = 2 x 2 x 3 x 5 = 2² x 3 x 5

2. Pilih faktor prima:

   • Faktor prima yang muncul di kedua bilangan adalah 2 dan 5. (Angka 3 hanya ada di 60, jadi tidak kita pilih).
   • Untuk faktor 2, ada 2³ dan 2². Kita pilih yang pangkatnya paling kecil, yaitu 2².
   • Untuk faktor 5, ada 5 (dari 40) dan 5 (dari 60). Keduanya pangkat 1, jadi kita ambil 5.

3. Hitung FPB:

   • FPB = 2² x 5
   • FPB = (2 x 2) x 5
   • FPB = 4 x 5 = 20

Contoh Soal 8: Berapakah FPB dari 18, 27, dan 45?

1. Faktorisasi Prima:

   • 18 = 2 x 3 x 3 = 2 x 3²
   • 27 = 3 x 3 x 3 = 3³
   • 45 = 3 x 3 x 5 = 3² x 5

2. Pilih faktor prima:

   • Faktor prima yang muncul di ketiga bilangan adalah 3. (Angka 2 hanya di 18, angka 5 hanya di 45, jadi tidak kita pilih).
   • Untuk faktor 3, ada 3² (dari 18), 3³ (dari 27), dan 3² (dari 45). Kita pilih yang pangkatnya paling kecil, yaitu 3².

3. Hitung FPB:

   • FPB = 3²
   • FPB = 3 x 3 = 9

Memecahkan Soal Cerita KPK dan FPB

Ini bagian yang paling seru! KPK dan FPB seringkali muncul dalam bentuk soal cerita. Kuncinya adalah bisa membedakan kapan menggunakan KPK dan kapan menggunakan FPB.

Indikator Soal Cerita KPK (Biasanya tentang jadwal, pertemuan, atau kejadian yang berulang)

• Kata kunci: "Setiap berapa hari sekali", "bersama-sama lagi", "bertemu kembali", "kapan mereka akan…", "paling cepat".
• Ciri-ciri: Mencari waktu atau jumlah di masa depan ketika suatu peristiwa akan terjadi secara bersamaan lagi.

Contoh Soal Cerita 9 (KPK):
Andi les renang setiap 4 hari sekali. Budi les renang setiap 6 hari sekali. Jika hari ini mereka les renang bersama-sama, berapa hari lagi mereka akan les renang bersama-sama untuk kedua kalinya?

Penyelesaian:
Ini adalah soal KPK karena kita mencari "kapan mereka akan bersama-sama lagi".

1. Faktorisasi Prima:
   • 4 = 2 x 2 = 2²
   • 6 = 2 x 3
2. KPK:
   • Ambil semua faktor prima dengan pangkat terbesar: 2² x 3
   • KPK = 4 x 3 = 12

Jadi, Andi dan Budi akan les renang bersama-sama lagi 12 hari kemudian.

Contoh Soal Cerita 10 (KPK):
Lampu A menyala setiap 3 detik. Lampu B menyala setiap 5 detik. Jika kedua lampu menyala bersamaan pada pukul 09.00, pada pukul berapa kedua lampu akan menyala bersamaan lagi?

Penyelesaian:
Ini soal KPK karena mencari "kapan menyala bersamaan lagi".

1. Faktorisasi Prima:
   • 3 = 3
   • 5 = 5
2. KPK:
   • Ambil semua faktor prima: 3 x 5 = 15

Jadi, kedua lampu akan menyala bersamaan lagi setiap 15 detik.
Jika pertama kali menyala bersamaan pukul 09.00.00, maka kedua lampu akan menyala bersamaan lagi pada pukul 09.00.15 (09 lewat 15 detik).

Indikator Soal Cerita FPB (Biasanya tentang pembagian, pengelompokan, atau ukuran terbesar)

• Kata kunci: "Dibagi rata", "sama banyak", "paling banyak", "jumlah kelompok terbesar", "ukuran terpanjang/terbesar yang sama".
• Ciri-ciri: Mencari jumlah terbesar yang bisa membagi rata beberapa benda, atau ukuran paling besar untuk suatu kelompok.

Contoh Soal Cerita 11 (FPB):
Bu guru memiliki 24 pensil dan 30 buku. Pensil dan buku tersebut akan dibagikan kepada sejumlah siswa sama banyak. Berapa paling banyak siswa yang bisa menerima pensil dan buku tersebut?

Penyelesaian:
Ini adalah soal FPB karena kita mencari "berapa paling banyak siswa" yang bisa menerima barang "sama banyak".

1. Faktorisasi Prima:
   • 24 = 2 x 2 x 2 x 3 = 2³ x 3
   • 30 = 2 x 3 x 5
2. FPB:
   • Pilih faktor prima yang sama dengan pangkat terkecil: 2 (pangkat 1) dan 3 (pangkat 1).
   • FPB = 2 x 3 = 6

Jadi, paling banyak ada 6 siswa yang bisa menerima pensil dan buku tersebut sama banyak.
(Setiap siswa akan menerima 24:6 = 4 pensil dan 30:6 = 5 buku).

Contoh Soal Cerita 12 (FPB):
Dito mempunyai 45 permen dan 60 cokelat. Ia ingin membuat parsel sebanyak-banyaknya dengan isi permen dan cokelat yang sama banyak di setiap parsel. Berapa parsel yang bisa Dito buat?

Penyelesaian:
Ini soal FPB karena kita mencari "berapa parsel sebanyak-banyaknya" dengan isi yang "sama banyak".

1. Faktorisasi Prima:
   • 45 = 3 x 3 x 5 = 3² x 5
   • 60 = 2 x 2 x 3 x 5 = 2² x 3 x 5
2. FPB:
   • Pilih faktor prima yang sama dengan pangkat terkecil: 3 (pangkat 1) dan 5 (pangkat 1).
   • FPB = 3 x 5 = 15

Jadi, Dito bisa membuat paling banyak 15 parsel.
(Setiap parsel berisi 45:15 = 3 permen dan 60:15 = 4 cokelat).

Tips Belajar KPK dan FPB Agar Lebih Asyik!

1. Pahami Konsep Dasar: Jangan terburu-buru menghitung KPK dan FPB kalau belum paham bilangan prima, faktorisasi, kelipatan, dan faktor. Ini kuncinya!
2. Gunakan Pohon Faktor: Ini adalah alat yang sangat membantu. Latih terus membuat pohon faktor sampai lancar.
3. Latihan Teratur: Semakin sering berlatih, semakin mudah kamu akan memahami dan mengingat caranya.
4. Buat Catatan Kecil: Tuliskan perbedaan cara mencari KPK dan FPB (KPK: semua faktor, pangkat terbesar. FPB: faktor yang sama, pangkat terkecil). Tempel di meja belajarmu!
5. Minta Bantuan: Jangan malu bertanya kepada guru, orang tua, atau kakak jika ada yang tidak kamu pahami. Mereka pasti senang membantumu!
6. Coba Buat Soal Sendiri: Ini cara yang bagus untuk menguji pemahamanmu.

Penutup

Wah, tidak terasa kita sudah menyelesaikan petualangan seru belajar KPK dan FPB! Kalian semua hebat sudah mau membaca dan memahami artikel ini sampai akhir. Ingat, matematika itu seperti bermain teka-teki. Jika kita tahu aturannya, pasti jadi seru dan menyenangkan.

KPK dan FPB adalah dasar penting yang akan terus kalian gunakan di jenjang kelas yang lebih tinggi. Jadi, teruslah berlatih dan jangan pernah menyerah. Semangat belajar, Adik-adik! Kalian pasti bisa!